research
Active research lines (2014!!!! out-of-date... TODO):
The overall theme of my research is combining high-fidelity numerical computer models and experimental data in fluid dynamics. These two methods of studying fluids are often highly complementary, and unifying them promises broad benefits. The basic framework I use comes from mathematical statistics; the challenge is to develop numerical-statistical approaches and tools that exploit the capabilities of CFD fully and efficiently. Goals are to:
- Build estimates for the error in CFD due to numerical models - especially RANS.
- Regress experimental data fields accounting for local error measures while satisfying PDE constraints - e.g. divergence-free regression of PIV data.
- Fill-in gappy PIV fields using the Navier-Stokes simulations.
- Increase the time-resolution of tomographic PIV, and evaluate instantaneous pressure fields, again with Navier-Stokes.
- Reduce uncertainty in aeroelastic simulations with small amounts of data.
Predictive RANS simulation with stochastic error estimates
with Paola Cinnella (ENSAM, ParisTech) and Wouter Edeling
The turbulence closure model is the dominant source of error in most Reynolds Averaged Navier-Stokes (RANS) simulations, yet no reliable estimators of this error currently exist. This leads to a lack of confidence in the predictions of CFD. The introduction of better turbulence models does not help much, given the continued lack of a measure of accuracy.
We aim to develop stochastic, a posteriori error estimates, calibrated for a specific class of flow. Our estimates are based on variability in model closure coefficients across multiple flow scenarios (within the class), for multiple closure models. The variability is estimated using Bayesian calibration against experimental data for each scenario, and Bayesian Model-Scenario Averaging (BMSA) is used to collate the resulting posteriors, to obtain a stochastic estimate of a Quantity of Interest (QoI) in an unmeasured (prediction) scenario.
So far we've demonstrated the effectiveness of the methodology for the class of flows consisting of turbulent boundary layers at a variety of pressure-gradients. We're now aiming for more complex flows with the goal of industrial relevance.
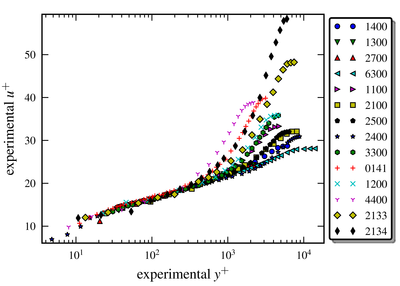
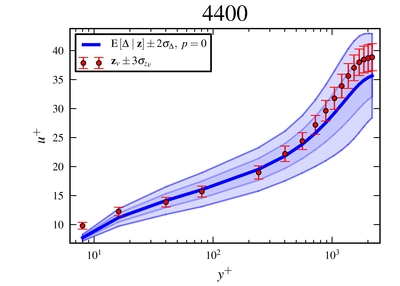
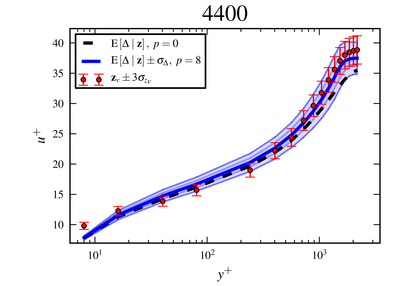
Stochastic processes for experimental data reconstruction
with Jouke de Baar, Iliass Azijli
TODO.Deterministic flow reconstruction with Navier-Stokes
with Fulvio Scarano and Jan Schneiders
TODO.Bayesian structural model updating in aeroelasticity
with Rakesh Sarma and Jouke de Baar
TODO.Surrogate modelling for uncertainty quantification/optimization
with Andrea Resmini and Jacques Peter (ONERA)
TODO.Past research lines:
- Least-squares finite element methods (LSFEM) for assimilation of experimental data into CFD. First applications are intended to be to Particle Image Velocimetry (PIV) data produced by the experimental half of the Aerodynamics Group.
- Uncertainty quantification in CFD using adaptive gradient-enhanced Kriging response surfaces and sparse grid integration (paper).
- A posteriori error estimation and goal-oriented mesh adaptation for finite volume methods (paper).
- Applications of algebraic multigrid (AMG) to compressible flow, via defect correction (with Anna Naumovich) (paper).
- Adjoint discretization and solution methods for sensitivity analysis and aerodynamic design optimization (with Joel Brezillon) (paper).
- Linear frequency domain methods for modeling periodic time-dependant flows, with applications in aeroelasticity.
- Linear elasticity for extremely robust mesh deformation using finite element discretizations (paper).
- Implicit convergence acceleration methods for stationary problems (paper).