LPFP: The Linearised Potential Flat Plate solver

This program generates analytic solutions of the linearised potential equation for a flat-plate airfoil oscillating harmonically in plunge (h) and pitch (&theta). Specifically, the program computes the coefficients Lh , L&theta, Mh and M&theta for a range of velocities U and frequencies &omega. These coefficients can be used to construct the complete lift (L) and moment (M) response at a given U and &omega using the expressions:
where b is the half chord, M is defined positive clockwise, and the excitation is assumed to be harmonic, i.e:

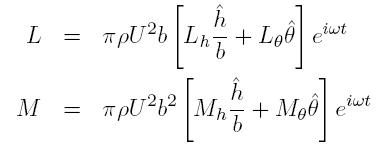
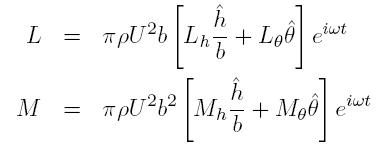If Mach=0 is selected, the program uses Theodorsen's (1934) linearised potential solution for unsteady incompressible flows to compute the coefficients. Otherwise, when Mach<1, Lin and Iliff's (2000) approximate solution to the Possio equation is used. Finally, if Mach>1, the program computes the supersonic solution of the linearised potential equation using the approach of Garrick and Rubinow (1946). Note that results from the linearised potential equation are not accurate in the transonic regime.

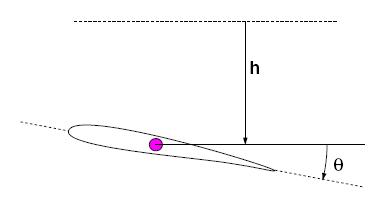
Two types of output can be produced using the forms below. In both cases, a value must be provided for the centre of rotation. This is measured in chord lengths from the mid-chord position (e.g for rotation about the quater chord enter -0.25).

If you require more information, contact S.J.Hulshoff@TUDelft.NL.

Coefficients for a fixed Mach number versus reduced frequency, k

Centre of rotation:

Mach number: or Mach = 0

Number of k s [max 250]:     k1: k2:


Coefficients on the U-&omega plane

Centre of rotation:     Chord length:

Speed of sound: or Mach = 0

Grid dimensions and ranges:

Number of velocities (U) [max 250]:         U1: U2:
Number of frequencies (&omega) [max 250]:     &omega1: &omega2: